1443. Minimum Time to Collect All Apples in a Tree
Difficulty: Medium
Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend in order to collect all apples in the tree starting at vertex 0 and coming back to this vertex.
The edges of the undirected tree are given in the array edges, where edges[i] = [from<sub style="display: inline;">i</sub>, to<sub style="display: inline;">i</sub>] means that exists an edge connecting the vertices from<sub style="display: inline;">i</sub> and to<sub style="display: inline;">i</sub>. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple, otherwise, it does not have any apple.
Example 1:
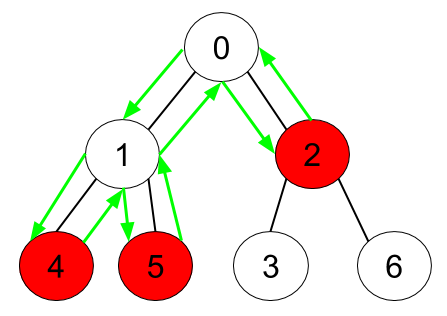
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
Example 2:
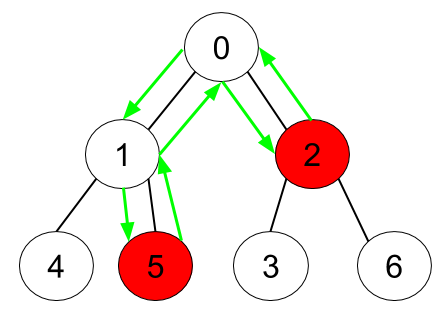
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
Example 3:
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0
Constraints:
1 <= n <= 10^5edges.length == n-1edges[i].length == 20 <= from<sub style="display: inline;">i</sub>, to<sub style="display: inline;">i</sub> <= n-1from<sub style="display: inline;">i</sub> < to<sub style="display: inline;">i</sub>hasApple.length == n
Solution
Language: Java
class Solution {
public static int minTime(int n, int[][] edges, List<Boolean> hasApple) {
HashMap<Integer, List<Integer>> graph = new HashMap<>();
for(int e = 0, len = edges.length; e < len; e++) {
graph.putIfAbsent(edges[e][0], new ArrayList<>());
graph.putIfAbsent(edges[e][1], new ArrayList<>());
graph.get(edges[e][0]).add(edges[e][1]);
graph.get(edges[e][1]).add(edges[e][0]);
}
boolean[] visited = new boolean[n];
visited[0] = true;
return dfs(0, hasApple, graph, visited);
}
private static int dfs(int u, List<Boolean> hasApple, HashMap<Integer, List<Integer>> graph, boolean[] visited) {
int time = 0;
for(int v : graph.get(u)) {
if(!visited[v]) {
visited[v] = true;
time += dfs(v, hasApple, graph, visited);
}
}
// if root then it does not matter whether it has apple or not
if(u == 0) return time;
// if children have apples does not matter whether this node has apple or not
// we have to travel that node any way
if (time > 0) return time + 2;
// if children does not have apples then we wil traverse this node only
// in case it has apple
return hasApple.get(u) ? 2 : 0;
}
}